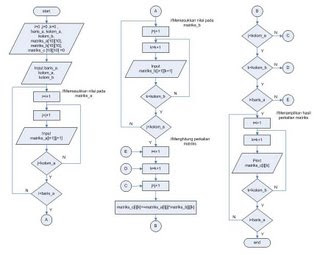
Algoritma Perkalian Matriks

Algoritma :

a.inisialisasi matrik_a[ ][ ], matrik_b[ ][ ], matrik_c[ ][ ], i=0, j=0, k=0, baris_a, kolom_a, kolom_b
b.inputkan baris_a, kolom_a, kolom_b
c.Proses looping untuk memasukkan nilai pada matrik_a :

1.untuk i=0 sampai dengan banyak baris_a-1, i=i+1
a)untuk j=0 sampai dengan banyaknya kolom_a-1, j=j+1
b)inputkan matrik_b[i+1][j+1]
c)Apakah j< kolom_a ? jika tidak, kembali ke proses c.1.a

2.Apakah i < baris_a ? jika tidak, kembali ke proses c 1.
d.Proses looping untuk memasukkan nilai pada matrik_b :

1.untuk j=0 sampai dengan banyak kolom_a-1, j=j+1
a)untuk k=0 sampai dengan banyaknya kolom_a-1, k=k+1
b)inputkan matrik_b[j+1][k+1]
c)Apakah k< kolom_b ? jika tidak, kembali ke proses d.1.a

2.Apakah j < kolom_a ? jika tidak, kembali ke proses d 1.
e.Proses looping untuk mengalikan matriks :
1.untuk i=0 sampai dengan banyak baris_a-1, i=i+1
a)untuk k=0 sampai dengan banyaknya kolom_b-1, k=k+1

i)untuk j=0 sampai dengan kolom_a -1, j=j+1
ii)matrik_c[i][k] + = matrik_a[i][j] * matrik_b[j][k]
iii)Apakah j< kolom_a ? jika tidak, kembali ke proses i)

b)Apakah k2.Apakah i < baris_a ? jika tidak, kembali ke proses e 1.
f.Proses looping untuk menampilkan matrik_c :

1.untuk i=0 sampai dengan banyak baris_a-1, i=i+1
a)untuk k=0 sampai dengan banyaknya kolom_b -1, k=k+1
b)Print matrik_c[i][k]
c)Apakah k< kolom_b ? jika tidak, kembali ke proses f.1.a

2.Apakah i < baris_a ? jika tidak, kembali ke proses f 1.
g.Program selesai.

Algoritma Penjumlahan Matriks

Algoritma :

a.inisialisasi matrik_a[ ][ ], matrik_b[ ][ ], matrik_c[ ][ ], a=0, b=0, i=0, j=0, baris, kolom

b.tentukan jumlah ordo matriks ( jumlah baris dan kolom)

c.Proses looping untuk memasukkan nilai pada matrik_a :

1.untuk a=0 sampai dengan banyaknya baris-1, a=a+1

a)untuk b=0 sampai dengan banyaknya kolom-1, b=b+1

b)inputkan matrik_a[a+1][b+1]

c)Apakah b<> jika tidak, kembali ke proses c.1.a

2.Apakah ad.Proses looping untuk memasukkan nilai pada matrik_b :

1.untuk i=0 sampai dengan banyak baris-1, i=i+1

a)untuk j=0 sampai dengan banyaknya kolom-1, j=j+1

b)inputkan matrik_b[i+1][j+1]

c)Apakah j<> jika tidak, kembali ke proses d.1.a

2.Apakah i <>

e.Proses looping untuk menambahkan matrik :

1.untuk a=0 sampai dengan banyaknya baris-1, a=a+1

a)untuk b=0 sampai dengan banyaknya kolom-1, b=b+1

b)matrik_c[a][b]= matrik_a[a+1][b+1] + matrik_b[i+1][j+1]

c)Apakah b<> jika tidak, kembali ke proses e.1. a

2.Apakah af.Proses looping untuk menampilkan matrik_c :

1.untuk a=0 sampai dengan banyaknya baris-1, a=a+1

a)untuk b=0 sampai dengan banyaknya kolom-1, b=b+1

b)Print matrik_c[a][b]c)Apakah b<>

2.Apakah ag.Program selesai.

Algoritma Konversi bilangan biner ke desimal

Algoritma :

a.inisialisasi biner[],i,hasil, dan desimal=0

b.inputkan bilangan biner

c.Proses loping :

1.untuk i=0 sampai dengan length (biner), i=i+1

2.keluarkan bilangan biner ke i lalu kalikan dengan 2i, masukkan ke hasil, dinyatakan dengan hasil.push(biner[i]* 2i

3.desimal+=hasil.pop

4.Print desimal

5.Apakah i = length (biner) ? jika tidak, Kembali ke proses c1

6.Program selesai.

Menentukan apakah suatu bilangan merupakan bilangan Prima atau bukan

Algoritma :

a.inisialisasi faktor, n, i, x

b.inputkan bilangan n

c.Proses looping :

1.untuk i=1 sampai dengan n, i=i+1

2.faktor =0

3.Proses looping :

a)untuk x=1 sampai dengan i, x=x+1

b)Apakah i%x=0 ? Jika iya, maka faktor=faktor +1.

c)Jika tidak, kembali ke proses 3 a)

dApakah x =i ? jika tidak, maka kembali ke proses 3 a)

4.pakah i= n ? jika tidak, kembali ke proses c1

d.Apakah faktor =2 ? jika iya, print ”Bilangan prima”

e.Jika tidak, print ” Bukan bilangan prima ”

f.Program selesai.

Algoritma menampilkan bilangan Fibbonaci

Algoritma :

a.inisialisasi N=20

b.inisialisasi fib[N]={1,1},temp=0,i ,n

c.Inputkan jumlah bilangan yang akan ditampilkan, masukkan ke variable n

d.Tampilkan fib[0] dan fib[1] yaitu {1} dan {1}

e.Proses looping :

1.Untuk i=0 sampai dengan n-2,i=i+1

2.Temp=temp+1

3.Fib[temp+1]=fib[i] + fib[i+1]

4.Print fib[temp+1]

5.Kembali ke proses e1.

f.Selesai

Dasar Algoritma dan Pemrograman

Definisi Algoritma

“Algoritma adalah urutan langkah-langkah logis penyelesaian masalah yang disusun secara sistematis dan logis”.

Kata Logis merupakan kata kunci dalam Algoritma. Langkah-langkah dalam Algoritma
harus logis dan harus dapat ditentukan bernilai salah atau benar.

Algoritma Merupakan Jantung Ilmu Informatika

Algoritma adalah jantung ilmu komputer atau informatika. Banyak cabang ilmu computer yang diacu dalam terminologi algoritma. Namun, jangan beranggapan algoritma selalu identik dengan ilmu komputer saja. Dalam kehidupan sehari-haripun banyak terdapat proses yang dinyatakan dalam suatu algoritma.

Cara-cara membuat kue atau masakan yang dinyatakan dalam suatu resep juga dapat disebut sebagai algoritma. Pada setiap resep selalu ada urutan langkah-lankah membuat masakan. Bila langkah-langkahnya tidak logis, tidak dapat dihasilkan masakan yang diinginkan. Ibu-ibu yang mencoba suatu resep masakan akan membaca satu per satu langkah-langkah pembuatannya lalu ia mengerjakan proses sesuai yang ia baca. S

ecara umum, pihak (benda) yang mengerjakan proses disebut pemroses (processor). Pemroses tersebut dapat berupa manusia, komputer, robot atau alatalat elektronik lainnya. Pemroses melakukan suatu proses dengan melaksanakan atau “mengeksekusi” algoritma yang menjabarkan proses tersebut. Melaksanakan Algoritma berarti mengerjakan langkah-langkah di dalam Algoritma tersebut. Pemroses mengerjakan proses sesuai dengan algoritma yang diberikan kepadanya. Juru masak membuat kue berdasarkan resep yang diberikan kepadanya, pianis memainkan lagu berdasarkan papan not balok.

Karena itu suatu Algoritma harus dinyatakan dalam bentuk yang dapat dimengerti oleh pemroses.

Jadi suatu pemroses harus :
1. Mengerti setiap langkah dalam Algoritma
2. Mengerjakan operasi yang bersesuaian dengan langkah tersebut.
Mekanisme Pelaksanan Algoritma Oleh Pemroses

Komputer hanyalah salah satu pemroses. Agar dapat dilaksanakan oleh komputer,
algoritma hasrus ditulis dalam notasi bahasa pemrograman sehingga dinamakan program.

Jadi program adalah prwujudan atau implementasi teknis Algoritma yang ditulis dalam bahasa pemrogaman tertentu sehingga dapat dilaksanakan oleh komputer.

Ciri penting algoritma
• Algoritma harus berhenti setelah mengerjakan sejumlah langkah terbatas.
• Setiap langkah harus didefinisikan dengan tepat dan tidak berarti-dua (Ambiguitas).
• Algoritma memiliki nol atau lebih masukkan.
• Algoritma memiliki nol atau lebih keluaran.
• algoritma harus efektif (setiap langkah harus sederhana sehingga dapat dikerjakan dalam waktu yang masuk akal).

Pengertian ALGORITMA

Algoritma

Diagram Alur sering digunakan untuk menggambarkan sebuah algoritma.

Dalam matematika dan komputasi, algoritma merupakan kumpulan perintah untuk menyelesaikan suatu masalah. Perintah-perintah ini dapat diterjemahkan secara bertahap dari awal hingga akhir. Masalah tersebut dapat berupa apa saja, dengan catatan untuk setiap masalah, ada kriteria kondisi awal yang harus dipenuhi sebelum menjalankan algoritma. Algoritma akan dapat selalu berakhir untuk semua kondisi awal yang memenuhi kriteria, dalam hal ini berbeda dengan heuristik. Algoritma sering mempunyai langkah pengulangan (iterasi) atau memerlukan keputusan (logika Boolean dan perbandingan) sampai tugasnya selesai.

Desain dan analisis algoritma adalah suatu cabang khusus dalam ilmu komputer yang mempelajari karakteristik dan performa dari suatu algoritma dalam menyelesaikan masalah, terlepas dari implementasi algoritma tersebut. Dalam cabang disiplin ini algoritma dipelajari secara abstrak, terlepas dari sistem komputer atau bahasa pemrograman yang digunakan. Algoritma yang berbeda dapat diterapkan pada suatu masalah dengan kriteria yang sama.

Kompleksitas dari suatu algoritma merupakan ukuran seberapa banyak komputasi yang dibutuhkan algoritma tersebut untuk menyelesaikan masalah. Secara informal, algoritma yang dapat menyelesaikan suatu permasalahan dalam waktu yang singkat memiliki kompleksitas yang rendah, sementara algoritma yang membutuhkan waktu lama untuk menyelesaikan masalahnya mempunyai kompleksitas yang tinggi.

Sejarah istilah "algoritma"Kata algoritma berasal dari latinisasi nama seorang ahli matematika dari Uzbekistan Al Khawārizmi (hidup sekitar abad ke-9), sebagaimana tercantum pada terjemahan karyanya dalam bahasa latin dari abad ke-12 "Algorithmi de numero Indorum". Pada awalnya kata algorisma adalah istilah yang merujuk kepada aturan-aturan aritmetis untuk menyelesaikan persoalan dengan menggunakan bilangan numerik arab (sebenarnya dari India, seperti tertulis pada judul di atas). Pada abad ke-18, istilah ini berkembang menjadi algoritma, yang mencakup semua prosedur atau urutan langkah yang jelas dan diperlukan untuk menyelesaikan suatu permasalahan.

Jenis-jenis Algoritma

Terdapat beragam klasifikasi algoritma dan setiap klasifikasi mempunyai alasan tersendiri. Salah satu cara untuk melakukan klasifikasi jenis-jenis algoritma adalah dengan memperhatikan paradigma dan metode yang digunakan untuk mendesain algoritma tersebut. Beberapa paradigma yang digunakan dalam menyusun suatu algoritma akan dipaparkan dibagian ini. Masing-masing paradigma dapat digunakan dalam banyak algoritma yang berbeda.

Divide and Conquer, paradigma untuk membagi suatu permasalahan besar menjadi permasalahan-permasalahan yang lebih kecil. Pembagian masalah ini dilakukan terus menerus sampai ditemukan bagian masalah kecil yang mudah untuk dipecahkan. Singkatnya menyelesaikan keseluruhan masalah dengan membagi masalah besar dan kemudian memecahkan permasalahan-permasalahan kecil yang terbentuk.

Dynamic programming, paradigma pemrograman dinamik akan sesuai jika digunakan pada suatu masalah yang mengandung sub-struktur yang optimal (, dan mengandung beberapa bagian permasalahan yang tumpang tindih . Paradigma ini sekilas terlihat mirip dengan paradigma Divide and Conquer, sama-sama mencoba untuk membagi permasalahan menjadi sub permasalahan yang lebih kecil, tapi secara intrinsik ada perbedaan dari karakter permasalahan yang dihadapi.

Metode serakah. Sebuah algoritma serakah mirip dengan sebuah Pemrograman dinamik, bedanya jawaban dari submasalah tidak perlu diketahui dalam setiap tahap;

dan menggunakan pilihan "serakah" apa yang dilihat terbaik pada saat itu.